Devoir Maison
Exercice 1
Calculer les dérivées des fonctions suivantes et simplifier (simplifier ne signifie pas forcément développer !):
|
1
\(f (x) = x \sqrt{x} + 2\)
|
2
\(g (x) = \frac{2 x - 1}{3 x + 2}\)
|
|
3
\(h (x) = \sqrt{x^2 + 2x +1}\)
|
4
\(k (x) = (x+1)(x-3)^4\)
|
Exercice 2
Calculer les limites suivantes. Enoncer correctement le théorème utilisé si besoin.
|
1
\(\lim\limits_{x \rightarrow -\infty} -2 x^3 + 3x - 11 \)
|
2
\(\lim\limits_{x \rightarrow +\infty} \frac{x^2 - 2x - 1}{3x+1} \)
|
3
\(\lim\limits_{x \rightarrow +\infty} x^2 cos (2x) - 2 \)
|
|
4
\(\lim\limits_{x \rightarrow +\infty} \frac{cos (2x)}{x+1} - 1 \)
|
5
\(\lim\limits_{x \rightarrow +\infty} \sqrt{\frac{1}{x^2+1}} \)
|
6
\(\lim\limits_{x \rightarrow -\infty} (2-\frac{1}{x} + x)^3 \)
|
Exercice 3
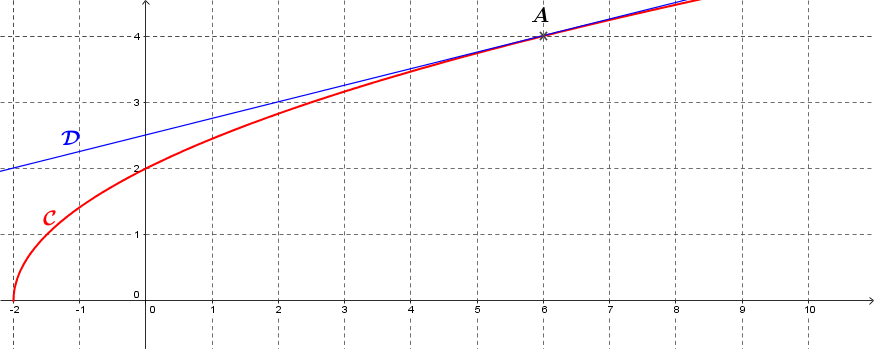
On représente ci-dessous la courbe \(\mathcal{C}\) de la fonction définie sur \(I = [-2;+\infty[\) par \(f (x)=\sqrt{2x+4}\), ainsi que la droite \(\mathcal{D}\) d'équation \(y = \frac{x}{4} + \frac{5}{2}\).

1
Soit \(A (6,4)\). Justifier que la courbe \(\mathcal{C}\) et la droite \(\mathcal{D}\) passent toutes les deux par \(A\).
2
Démontrer que la droite \(\mathcal{D}\) est la tangente à la courbe \(\mathcal{C}\) en \(x=6\).
3
Etudier les variations de la fonction \(f\) sur \(I = [-2;+\infty[\).
4
On considère la fonction \(g (x) = f (x) - \frac{x}{4} - \frac{5}{2}\).
a
Etudier le signe de la fonction \(g\).
b
En déduire la position de la courbe \(\mathcal{C}\) par rapport à la droite \(D\) sur \([-2;+\infty[\)
Exercice 4
Mettre sous forme algébriques les complexes suivants :
|
1
\(z_1 = (3i - 1)^2 (i - 2)\)
|
2
\(z_2=\frac{2+i}{4-i}\)
|
Exercice 5
Placer dans un repère orthonormé \((O;\vec{u};\vec{v})\) les points \(A,B,C,D\) d'affixes : $$ z_A=-2 ; z_B=-1-2i ; z_C=3+i ; z_D=2+3i $$ Quelle est la nature du quadrilatère \(ABCD\) (justifier par le calcul).
Exercice 6
Résoudre les équations suivantes d'inconnue \(z\) :
|
1
\(z^2+5=-4z\)
|
2
\(\frac{1+z}{z-6}=4 z\)
|